基础知识

数据的表示

Scalar: a 标量，0维
Vector: a[i]， 向量，1维
Matrix: a[i,j]， 矩阵，2维
Tensor: a[i,j,k]， 张量，多维

Tensor和 Graph的关系:
Graphs over time -> 3rd order tensors

Knowledge Graphs: a directed heterogeneous multigraph whose node and relation types have domain-specific semantics （Vertices: Entities, Edges: Predicates）
有向、异源、对关系图

为什么要进行嵌入？

Meaningful non-numerical representations are highly important, e.g., languages with discrete representations, graphs, shapes

But, Most inference models, e.g., SVM, NN, Reg., etc., are designed for vector-space representable quantities
=>
To benefits from these models, we need to convert non-numeric representations to numeric representations

简单的说，就是将高维的离散信息转化为低维的连续数据，并且保持其信息的完整性，用于后续的建模分析。

嵌入

定义:
Mapping of a discrete variable to a vector of continuous numbers such that semantic/abstract similarities are encoded in terms of geometric distances

• Low-dimensional -> Mitigate redundancy, curse of dimensionality(避免维度灾难)
• Embeddings provide a generalizable context about the overall
graph that can be used for interference, e.g., relations.

图嵌入

Given entities & predicates, find mappings for entities and links (predicate (s,r,t))
就是将实体或者关系以向量的形式表达。

图嵌入方法

SVD

• Decomposition in terms of singular values
• V, U: orthogonal matrices

Deep Graph Embeddings

Skip-gram: DeepWalk, Node2Vec
思想:
Sample a set of paths with random walk from node 𝑣i
Adjacent Nodes are Similar and should have similar embeddings. The frequency of co-occurrence in random walks is an indicator of node similarity.

• Hierarchical Softmax (DeepWalk)
• Negative Sampling (Node2Vec)

其他算法

Metapath2Vec: heterogenous graph
LINE: 1st order + 2nd order proximity
UltimateWalk: closed form, unifies DeepWalk and Node2Vec reconstruct W,
AutoEncoder: similar to SVD
Struc2Vec: focuses on structural similarity
GCN: interesting! borrowed the idea from CNN

图嵌入应用

• Reconstruction / Fact checking: Triples completion: (s,?,t)
• Classification: Triples classification: (s,r,t)
• Featurizing: Link prediction, Recommendation

Tensor与图嵌入

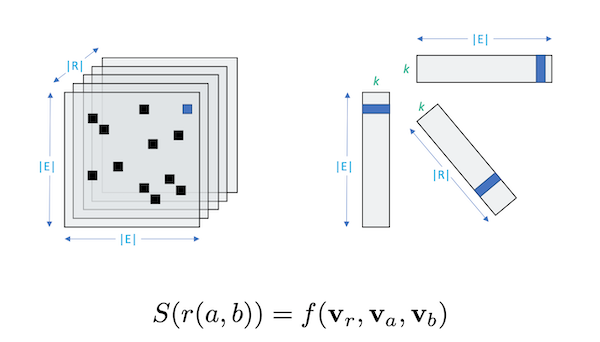
PARAFAC

针对图张量的分解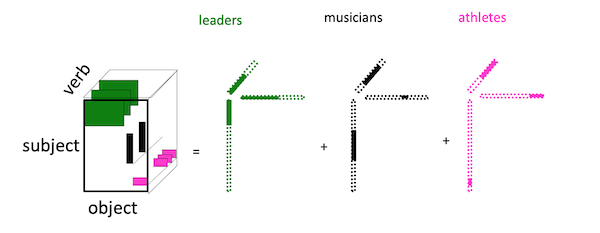

知识图谱嵌入

Problem statement:
How to enforce KG structures on the embedding representations?

Solution: Triple scoring

Loss: what shall we optimize?

Triple Scoring

What is the relationship among sub (h), pred (r), and obj (t)? • Addition: h + r =?= t
表示实体关系向量间的关系。

1. Addition: h + r =?= t
2. Multiplication: h ⚬ r =?= t

Addition

查看 h + r 是否 = t

TransE算法:
score(h,r,t) = – ||h+r-t|| 返回结果二范式的负值

‘Merkel’: h=(1, 0, 0)
‘Beatles’: t =(0, 0, 1)
‘plays_bass’: r =(0, 0, 1) 
score(h,r,t)=- ||h+ t− r|| = -1

缺陷:
从公式就可以看出，该算法不适用于一对多的关系

TransH:
Project to relation-specific hyperplanes

TransR:
Translate to relation-specific space

Multiplication

查看 h ⚬ r 是否 = t

RESCAL算法, score(h,r,t) = h.T ⚬ Wr ⚬ t
缺陷: Too many parameters

DistMult算法, score(h,r,t) = h.T ⚬ diag(Wr) ⚬ t
好处: Simplify RESCAL by using a diagonal matrix
缺陷: Cannot deal with asymmetric relations!

ComplEx算法: score(h,r,t) = Re(h.T ⚬ diag(Wr) ⚬ t)
Extend DistMult by introducing complex value embedding, so can handle asymmetric relations

Loss

Closed world assumption: square loss